今日題目

題目連結：53. Maximum Subarray
題目主題：Array, Divide and Conquer, Dynamic Programming

這次的題目跟昨天一樣，但是使用的解法跟主題是完全不同的，昨天使用的是 Divide and Conquer，今天會使用 Dynamic Programming，體驗這個題目不同解法的感覺。

簡單說說 Dynamic Programming

Dynamic Programming 動態規劃，核心觀念是用空間來優化效能。使用時也會將問題分解成小問題，找到一個規律出來，最後將小問題的答案都儲存下來，每次往下一個問題找答案時可以使用前面存下來的答案來快速解決問題。

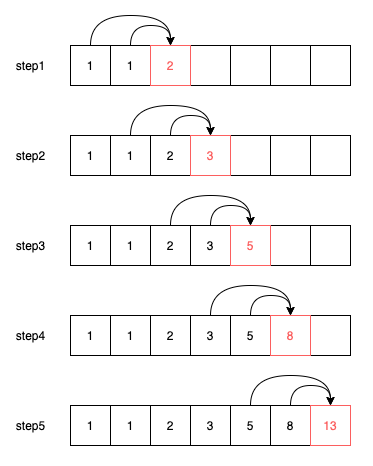
以費氏數列為例子，我們能找到的規律是一個數字一定會是前面兩個數字的加總，因此我們在計算過程將每次的結果都記錄下來，當算下一個數字時，只要拿前面兩個數字加總就可以得到答案了，運作過程如下：

題目解說

建議可以看看LeetCode原本的題目說明，這邊是用我的方式說明題目，參考就好。

題目會給一個 nums 數字陣列，目的是要找出 nums 中每個連續的子集合總和後最大的值，最終回傳這個最大的總和值。

約束：

• 1 <= nums.length <= 10的5次方
• -10的4次方 <= nums[i] <= 10的4次方

範例1

輸入: nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出: 6
解說: 
列出全部的連續子集合可能會有點多，這邊只舉幾個例子:
[-2] = -2
[-2,1,-3,4] = 0
[4,-1,2,1] = 6
[2,1,-5,4] = 2
[-2,1,-3,4,-1,2,1,-5,4] = 1
上面是連續的子集合的例子，每個加總後可以看到[4,-1,2,1]總和的6最大，因此最後輸出 6。

範例2

輸入: nums = [1]
輸出: 1
解說: 因為只有一個 1，因此最大也一定是 1。

範例3

輸入: nums = [5,4,-1,7,8]
輸出: 23
解說: 這個例子最大的就是[5,4,-1,7,8]加總後的23，因此最後輸出23。

建議到這邊先停下來，嘗試自己解解看，若沒有想法可再繼續走下去。

解題的想像

文字描述

1. 宣告兩個變數，預設約束最小值 -10的4次方 分別為：
   • currentMax: 記錄目前使用連續子集的加總。
   • maxSum: 記錄目前連續子集中加總的最大值。
2. 跑一個迴圈，將每個值走過一次，每圈處理內容如下：
   • currentMax + 目前的值。
   • 確認要保留的值，更新目前使用的連續子集加總。
   • 確認要保留的值，更新目前連續子集中加總的最大值。

圖解過程

範例：nums = [-3, 4, -1, 2, 1, -5, 4, -2]

上圖是預設狀態，我們會先宣告出 currentMax 及 maxSum，分別預設給他們約束的最小值 -10的4次方。

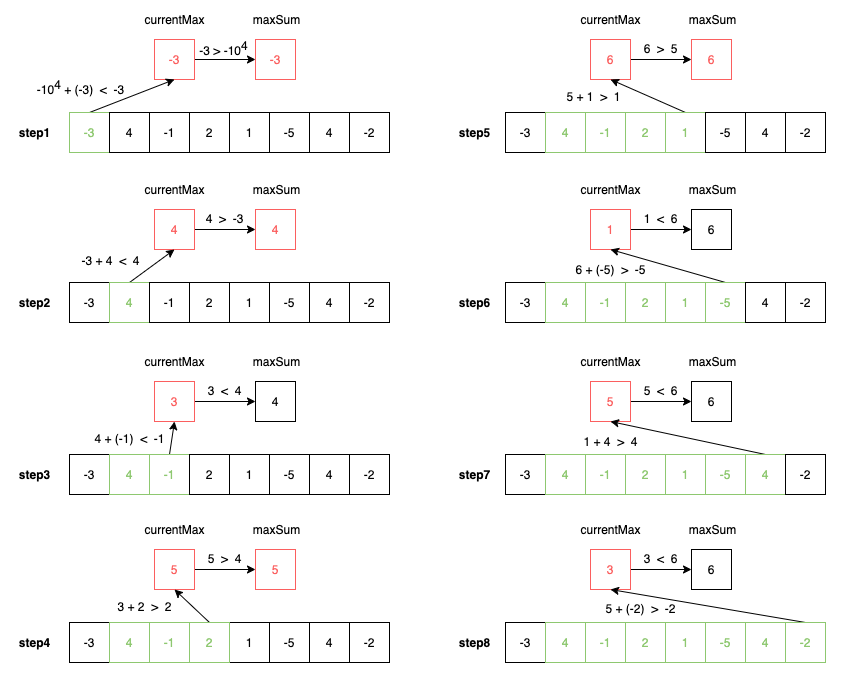
上圖是迴圈每一圈的處理過程，紅色方框代表是更新過的最大總和，綠色方框是目前使用的子集，可以先看 step1 ~ step2 的變化，會發現當目前子集的總和沒有大過現在的值，會保留現在的值，捨棄前面子集的總和，到了 step3 是直接從 4 開始往下去算總和，就不會把 -3 在算進來。

整體來看，可以看到在 step5 的時候，已經找到最大值 6 了，step6 ~ step8 的子集總和都沒有再出現更大的值，因此會保留 6 到最後，這也是最終這個範例的答案。

若因為沒想法而走到這邊，建議看完想像以後再給自己一次機會試一次。

程式碼撰寫

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        # 從最小值開始紀錄
        currentMax = -10 ** 4
        maxSum = -10 ** 4
        # 每一圈都取一個值
        for num in nums:
            # 更新目前使用的連續子集加總
            currentMax = currentMax+num if currentMax+num > num else num
            # 更新目前連續子集中加總的最大值
            maxSum = currentMax if currentMax > maxSum else maxSum
        return maxSum

希望您今天能瞭解到...

1. Dynamic Programming 基本概念
2. 53. Maximum Subarray 使用Dynamic Programming的解法

若內容有什麼問題或建議歡迎一起交流：）
感謝您今天願意花時間看完這篇文章~~~~

Next：572. Subtree of Another Tree